Phase portraits for systems of differential equations with complex Eigenvalues

How to sketch the phase portrait of a system of differential equations when we have Eigenvalues that are complex numbers

Now we want to look at the phase portraits of systems with complex Eigenvalues. Here’s what we need to know:

Krista King Math.jpg — Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

There are no linear trajectories for the system.
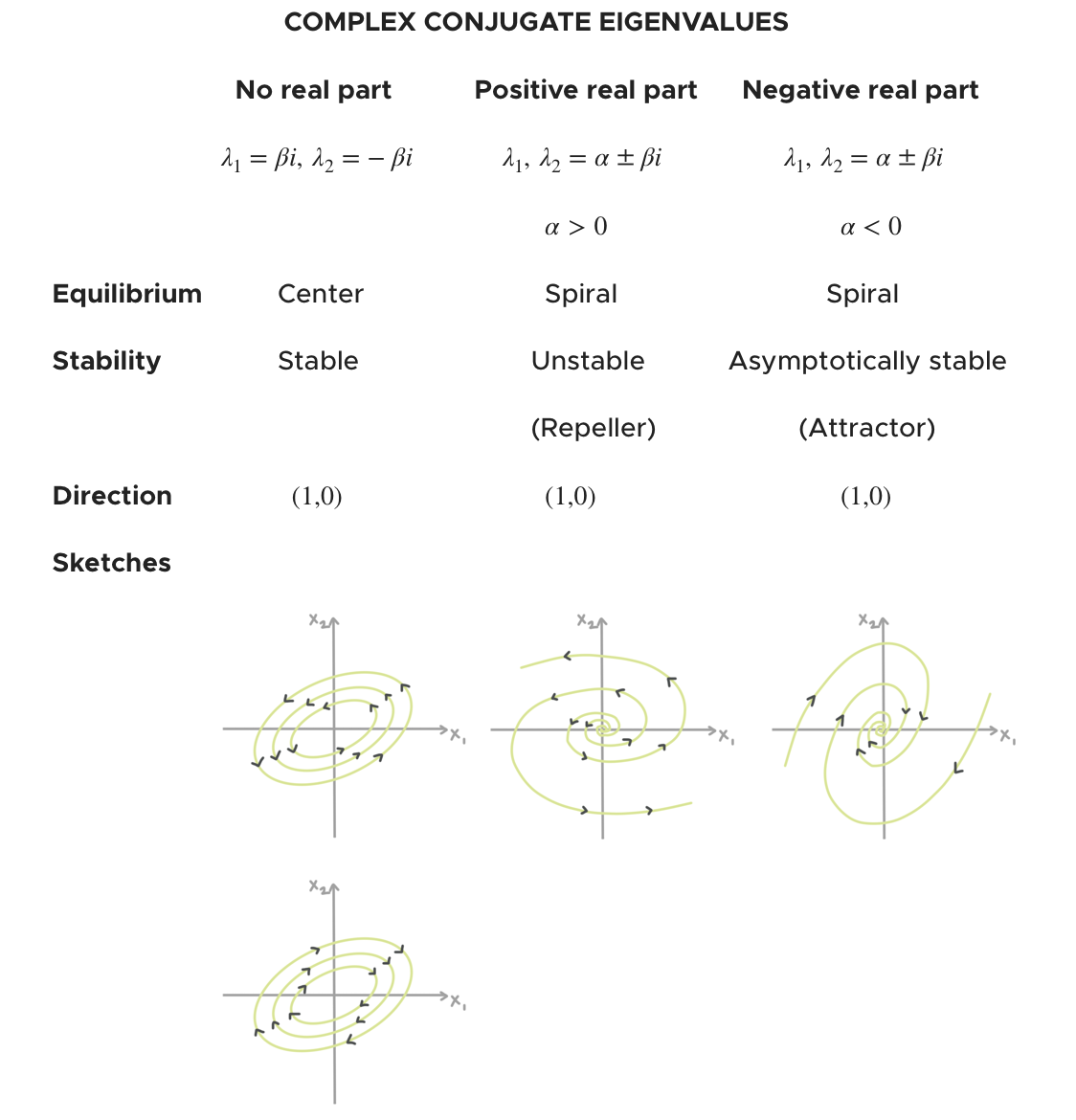
The equilibrium of a system with complex Eigenvalues that have no real part is a stable center around which the trajectories revolve, without ever getting closer to or further from equilibrium. The equilibrium of a system with complex Eigenvalues with a positive real part is an unstable spiral that repels all trajectories. The equilibrium of a system with complex Eigenvalues with a negative real part is an asymptotically stable spiral that attracts all trajectories.
To check for the direction of the trajectories for any case of complex conjugate Eigenvalues, we can use the ???(1,0)??? test, which means we’ll look at the direction at the point ???(1,0)???.

Below is a table that summarizes information about the phase portrait, based on the sign of the complex conjugate Eigenvalues.

Sketching the phase portrait step-by-step

Take the course

Want to learn more about Differential Equations? I have a step-by-step course for that. :)

Learn More

An example with a positive real part, giving an unstable spiral that repels all trajectories

Let’s do an example so that we can see how to build a phase portrait for complex conjugate Eigenvalues.

Example

Sketch the phase portrait of the system.

???x_1'=4x_1+5x_2???

???x_2'=-2x_1+6x_2???

This is one of the examples we looked at when we learned to solve homogeneous systems with complex conjugate Eigenvalues, and we found that the Eigenvalues for the system were ???\lambda_1=5+3i??? and ???\lambda_2=5-3i???.

These are Eigenvalues with a positive real part, ???\alpha=5>0???, which means we’re dealing with an unstable spiral that repels all trajectories.

If we test the vector ???\vec{x}=(1,0)??? in the matrix equation associated with the system, we get

To check for the direction of the trajectories for any case of complex conjugate Eigenvalues, we can use the (1,0) test, which means we’ll look at the direction at the point (1,0).

This ???(1,0)??? test tells us that the direction of the trajectory running through that point must have a direction toward ???(4,-2)??? (into the fourth quadrant), which means that the phase portrait must look something like