Polar coordinates vs. rectangular coordinates

Polar coordinates start with rectangular coordinates

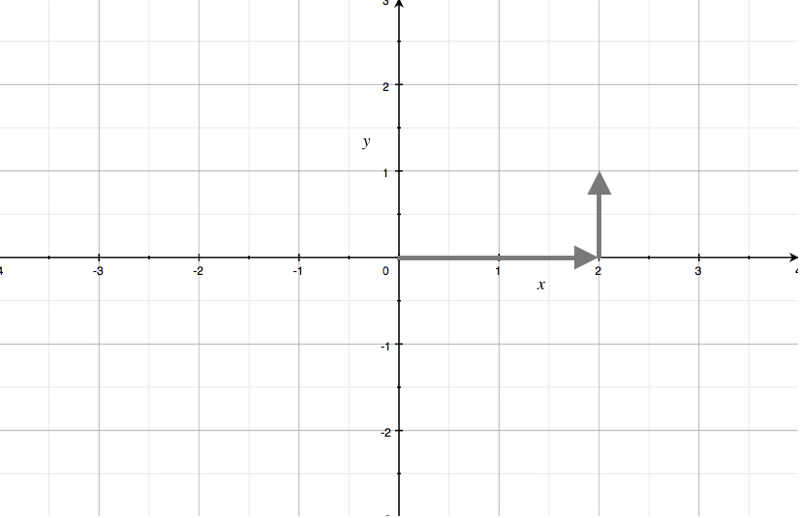
Rectangular coordinates, or cartesian coordinates, come in the form $(x,y)$.

It’s easy to remember that they’re called rectangular coordinates, because if you start at the origin and move first to the $x$-coordinate, and then to the $y$-coordinate, your path is a horizontal line, followed by a vertical line, which form two sides of a rectangle.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

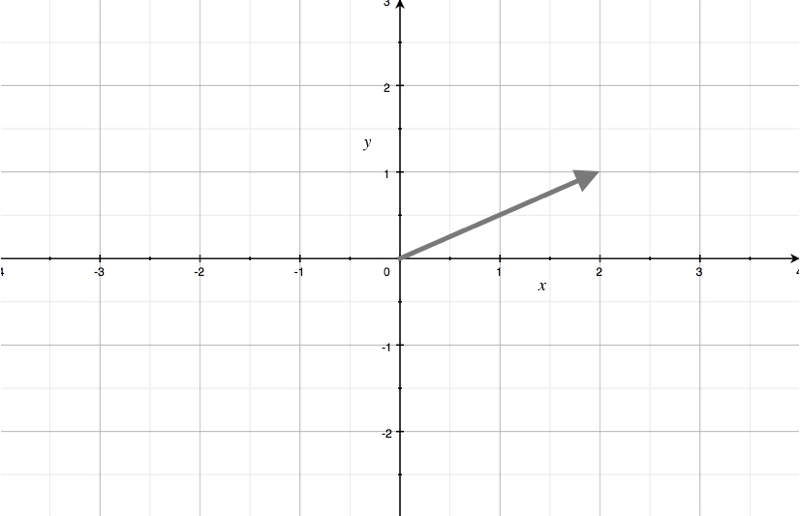
Polar coordinates, on the other hand, come in the form $(r,\theta)$. Instead of moving out from the origin using horizontal and vertical lines, we instead pick the angle $\theta$, which is the direction, and then move out from the origin a certain distance $r$.

Rectangular to polar

To convert rectangular coordinates to polar coordinates, we’ll use the conversion formulas

$x^2+y^2=r^2$

$x=r\cos{\theta}$

$y=r\sin{\theta}$

We’ll start by plugging the $x$ and $y$ values from the rectangular point into the left side of $x^2+y^2=r^2$, and we’ll get a value for $r$.

Then we’ll use

$r$ and the $x$-value and plug them into $x=r\cos{\theta}$

$r$ and the $y$-value and plug them into $y=r\sin{\theta}$.

The value of $\theta$ that turns out to be a solution to both equations is the value of $\theta$ we should use in our converted polar point.

Polar to rectangular

To convert polar coordinates to rectangular coordinates, we’ll use the conversion formulas

$x=r\cos{\theta}$

$y=r\sin{\theta}$

All we have to do is take the values of $r$ and $\theta$ from the polar point, plug them into the right sides of these conversion formulas, and solve for $x$ and $y$, the values we need for the equivalent rectangular coordinate point.

How to convert back and forth between polar and rectangular coordinates

---

Take the course

Want to learn more about Calculus 2? I have a step-by-step course for that. :)

---

Converting the rectangular point to a polar point

Example

Convert the rectangular point to a polar point.

$(1,-1)$

We’ll plug the $x$- and $y$-values from our rectangular point into $x^2+y^2=r^2$ to find $r$.

$x^2+y^2=r^2$

$(1)^2+(-1)^2=r^2$

$1+1=r^2$

$2=r^2$

$\sqrt{2}=r$

Note: There are multiple ways to indicate the same polar point. Even though $r=\pm\sqrt{2}$, we’re only using the positive solution because the negative solution will actually return the same polar point. This will always be true, so you can always get away with only using the positive solution for $r$.

Plugging $r=\sqrt{2}$ and $x=1$ into $x=r\cos{\theta}$ to find $\theta$, we get

$x=r\cos{\theta}$

$1=\sqrt{2}\cos{\theta}$

$\frac{1}{\sqrt{2}}=\cos{\theta}$

$\frac{1}{\sqrt{2}}\left(\frac{\sqrt{2}}{\sqrt{2}}\right)=\cos{\theta}$

$\frac{\sqrt{2}}{2}=\cos{\theta}$

$\theta=\frac{\pi}{4},\ \frac{7\pi}{4}$

and

$y=r\sin{\theta}$

$-1=\sqrt{2}\sin{\theta}$

$-\frac{1}{\sqrt{2}}=\sin{\theta}$

$-\frac{1}{\sqrt{2}}\left(\frac{\sqrt{2}}{\sqrt{2}}\right)=\sin{\theta}$

$-\frac{\sqrt{2}}{2}=\sin{\theta}$

$\theta=\frac{5\pi}{4},\ \frac{7\pi}{4}$

Since $\theta=7\pi/4$ is a solution to both equations, this is the one we’ll use.

The equivalent polar coordinate point is

$\left(\sqrt{2},\frac{7\pi}{4}\right)$

Instead of moving out from the origin using horizontal and vertical lines, we instead pick the angle, which is the direction, and then move out from the origin a certain distance.

Converting a polar point to a rectangular point

Example

Convert the polar point to a rectangular point.

$\left(1,\frac{\pi}{2}\right)$

We’ll use the conversion formulas, plugging $1$ in for $r$ and $\pi/2$ in for $\theta$. 

$x=r\cos{\theta}$

$x=1\cos{\frac{\pi}{2}}$

$x=0$

and

$y=r\sin{\theta}$

$y=1\sin{\frac{\pi}{2}}$

$y=1$

The equivalent rectangular coordinate point is $(0,1)$.

---

Get access to the complete Calculus 2 course

---