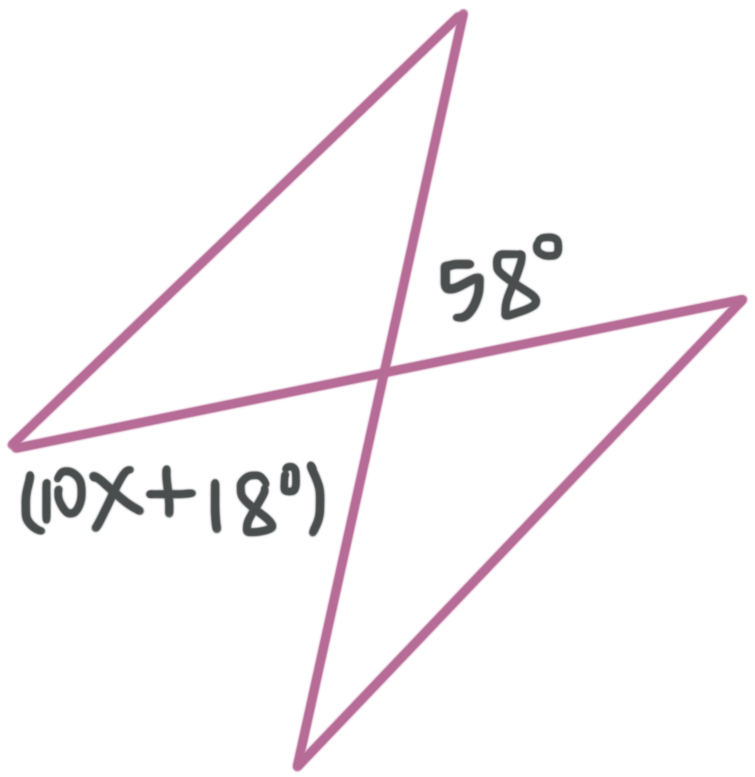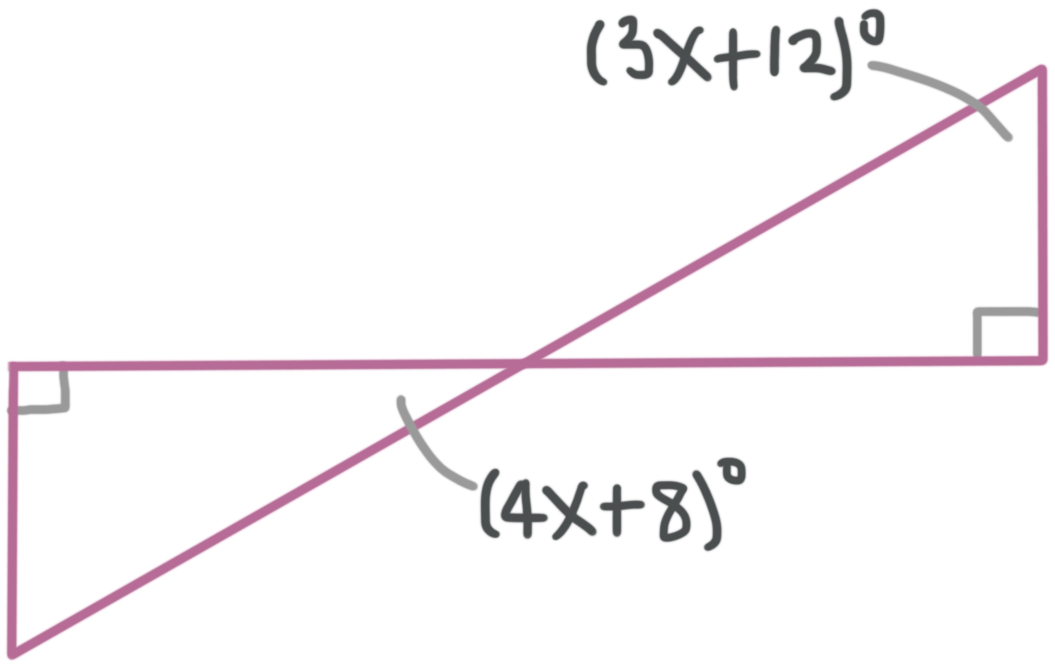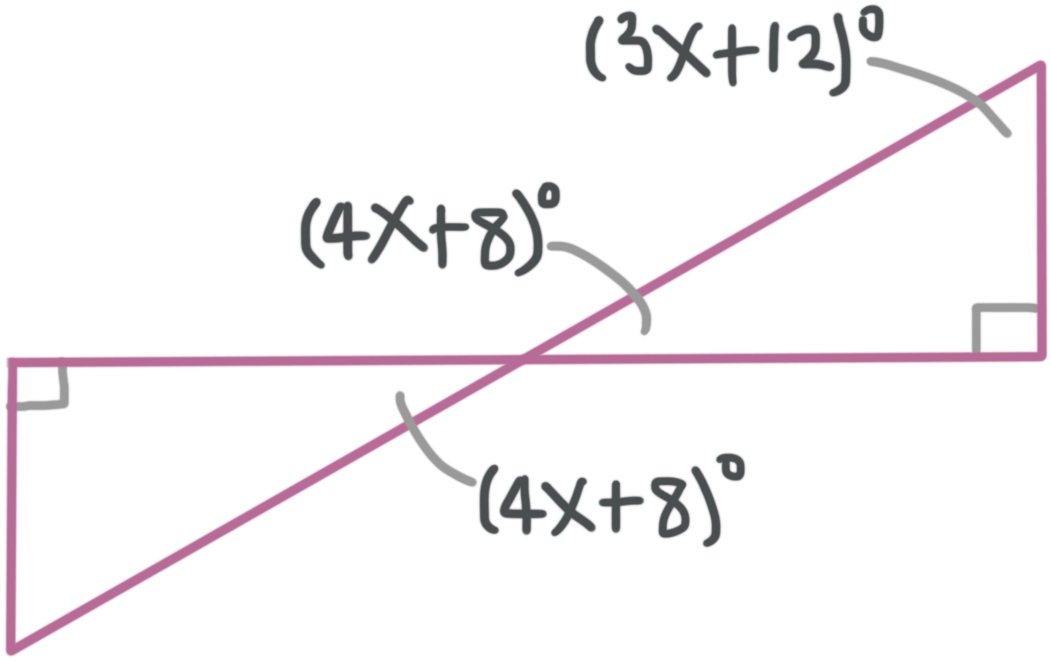Vertical angles as congruent angles
Vertical angles are congruent angles
In this lesson we’ll look at how to use vertical angles to solve problems.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
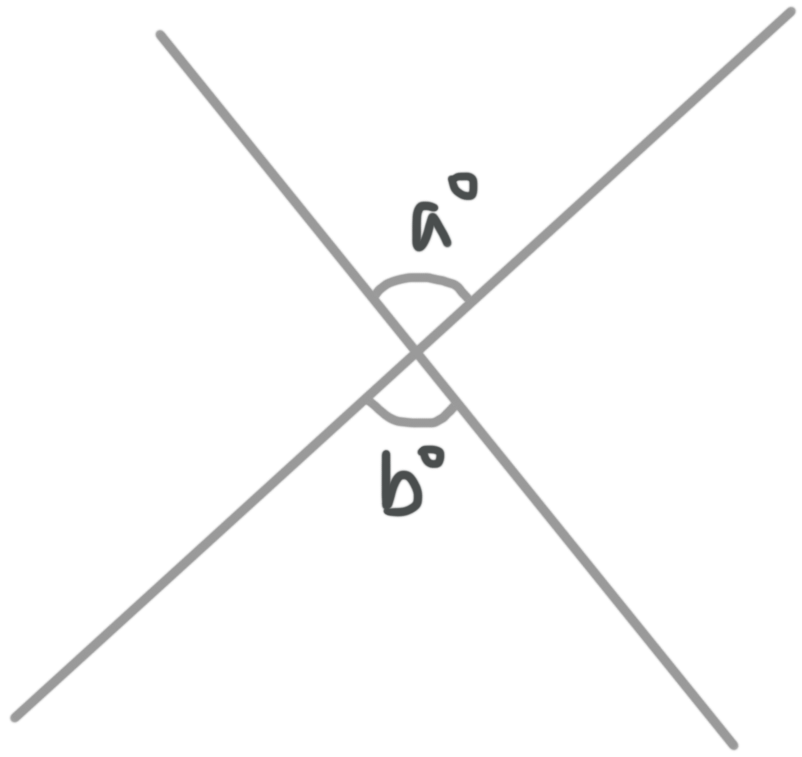
Vertical angles
Vertical angles are angles in opposite corners of intersecting lines, like these:
So vertical angles always share the same vertex, or corner point of the angle. They’re a special angle pair because their measures are always equal to one another. Therefore, from the diagram we can say
???a{}^\circ =b{}^\circ???
or
???\angle a\cong \angle b???
How to use vertical (and congruent) angles to solve geometry problems
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Vertical angles that include an unknown value
Example
Find the value of ???x???.
???58{}^\circ??? and ???(10x+18){}^\circ??? are vertical angles, and are therefore congruent, so we can set them equal to one another and solve for the variable.
???(10x+18){}^\circ =58{}^\circ???
???10x{}^\circ =40{}^\circ???
???x=4{}^\circ???
Let’s try another one.
Vertical angles are angles in opposite corners of intersecting lines.
Example
Solve for the variable.
Use the fact that vertical angles are congruent to complete the triangle on the right. The angle measuring ???(4x+8)^\circ??? has a vertical angle inside the triangle on the right.
The angles in a triangle sum to ???180{}^\circ???, so we can set up an equation to solve for the variable.
???(4x+8){}^\circ +(3x+12){}^\circ +90{}^\circ =180{}^\circ???
???7x{}^\circ +110{}^\circ =180{}^\circ???
???7x{}^\circ =70{}^\circ???
???x=10{}^\circ???