How to find the scalar and vector projections of one vector onto another

What are scalar and vector projections?

Scalar projections

The scalar projection of one vector onto another (also called the component of one vector along another), is

$\text{comp}_a{b}=\frac{a\cdot{b}}{|a|}$

where $a\cdot{b}$ is the dot product of the vectors $a$ and $b$, and $|a|$ is the length of $a$ (also called the magnitude of $a$).

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

Vector projections

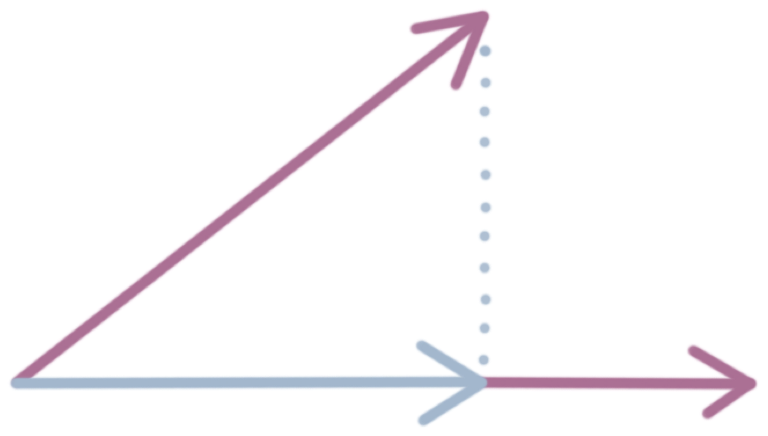
The vector projection of one vector onto another is like a shadow that one vector casts on another vector. For example, the projection of green onto orange is blue:

$\text{proj}_a{b}=\left(\frac{a\cdot{b}}{|a|}\right)\frac{a}{|a|}$

where $a\cdot{b}$ is the dot product of the vectors $a$ and $b$, and $|a|$ is the length of $a$ (also called the magnitude of $a$).

How to find the scalar and vector projections of one vector onto another

---

Take the course

Want to learn more about Calculus 3? I have a step-by-step course for that. :)

---

A step-by-step example of how to find the scalar projections and vector projections

Example

Find the scalar and vector projections of $b$ onto $a$.

$a=i+2j-3k$

$b=6i+j$

Since we use the value of the scalar projection in the formula for the vector projection, we’ll start by finding the scalar projection. We’ll need the dot product of $a$ and $b$ and the magnitude of $a$.

We’ll convert the given vector equations into the form

$a=\langle1,2,-3\rangle$

$b=\langle6,1,0\rangle$

We’ll take the dot product.

$a\cdot{b}=(1)(6)+(2)(1)+(-3)(0)$

$a\cdot{b}=6+2+0$

$a\cdot{b}=8$

Since we use the value of the scalar projection in the formula for the vector projection, we’ll start by finding the scalar projection.

We’ll find the magnitude (length) of $a$ using the distance formula. Remember, the terminal point of $a$ is $(1,2,-3)$ and the initial point of $a$ is $(0,0,0)$.

$|a|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}$

$|a|=\sqrt{(1-0)^2+(2-0)^2+(-3-0)^2}$

$|a|=\sqrt{1+4+9}$

$|a|=\sqrt{14}$

We’ll plug $a\cdot b$ and $|a|$ into the formula for the scalar projection.

$\text{comp}_a{b}=\frac{8}{\sqrt{14}}$

Since we have the scalar projection, we already have everything we need to find the vector projection.

$\text{proj}_a{b}=\left(\frac{8}{\sqrt{14}}\right)\frac{i+2j-3k}{\sqrt{14}}$

$\text{proj}_a{b}=\frac{8i+16j-24k}{14}$

$\text{proj}_a{b}=\frac{4i+8j-12k}{7}$

$\text{proj}_a{b}=\frac47i+\frac87j-\frac{12}{7}k$

To summarize our findings, we’ll say that

the scalar projection of $b$ onto $a$ is

$\text{comp}_a{b}=\frac{8}{\sqrt{14}}$

the vector projection of $b$ onto $a$ is

$\text{proj}_a{b}=\frac47i+\frac87j-\frac{12}{7}k$

---

Get access to the complete Calculus 3 course

---