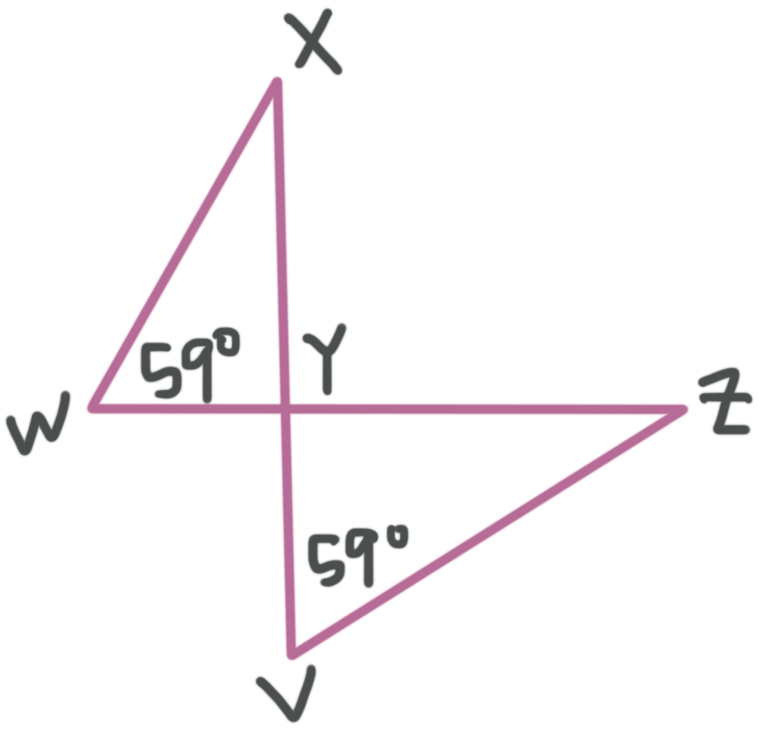Theorems for proving that triangles are similar
Similar figures are the same shape, but can be different sizes
In this lesson we’ll look at how to prove triangles are similar to one another.
In math, the word “similarity” has a very specific meaning.
Outside of math, when we say two things are similar, we just mean that they’re generally like one another.
But in math, to say two figures are similar means that they have exactly the same shape, but that they’re different sizes. Here are examples of similar squares, similar pentagons, and similar triangles:
Similar triangles
Similar triangles are the same shape but not the same size. Remember that if two triangles are both exactly the same shape, and exactly the same size, then they are identical and we say they’re “congruent.”
In a pair of similar triangles, all three corresponding angle pairs are congruent and corresponding side pairs are proportional. The symbol for similarity is ???\sim???, so if we want to say that triangles ???A??? and ???B??? are similar to one another, then we can write that as ???A\sim B???.
The triangles below are similar because the corresponding interior angles are congruent, and because the side lengths are proportional like this:
???\frac{a}{t}=\frac{b}{u}=\frac{c}{v}???
We’re going to look at three theorems that allow you to prove that triangles are similar.
Angle Angle (AA)
If a pair of triangles have two corresponding angles that are congruent, then we can prove that the triangles are similar. The reason is because, if you know two angles are congruent, then the third set of corresponding angles have to be congruent as well because the angles in a triangle always sum to ???180^\circ???.
Side Side Side (SSS)
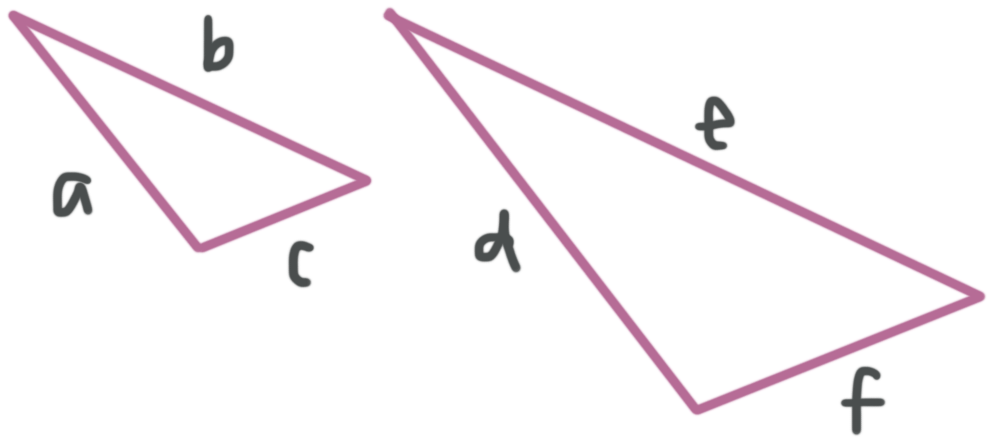
If a pair of triangles have three proportional corresponding sides, then we can prove that the triangles are similar. The reason is because, if the corresponding side lengths are all proportional, then that will force corresponding interior angle measures to be congruent, which means the triangles will be similar.
???\frac{a}{d}=\frac{b}{e}=\frac{c}{f}???
Side Angle Side (SAS)
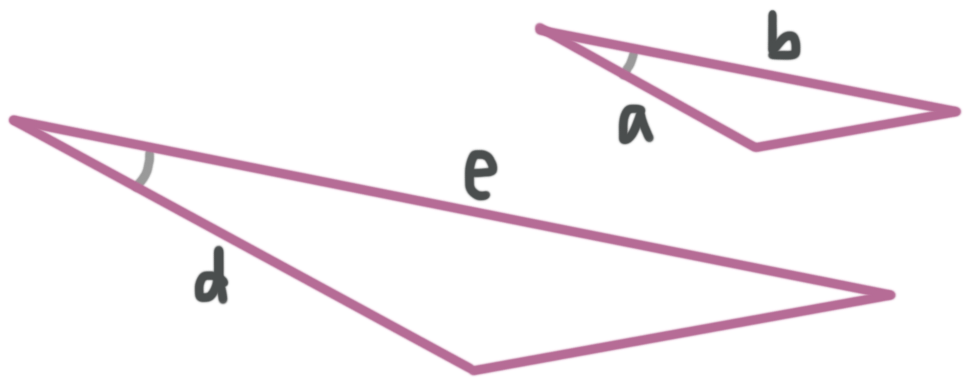
If a pair of triangles have one pair of corresponding congruent angles, sandwiched between two pairs of proportional sides, then we can prove that the triangles are similar.
???\frac{a}{d}=\frac{b}{e}???
Theorems for proving that two triangles are similar
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Which theorem proves that the triangles are similar?
Example
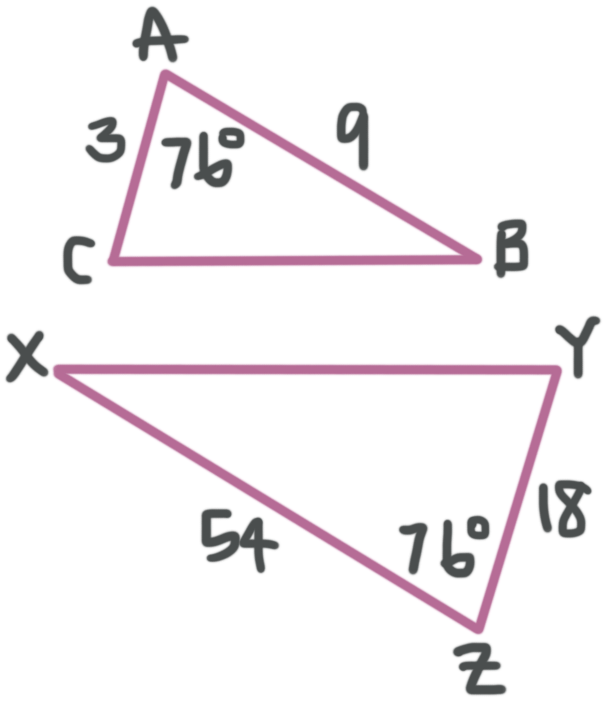
Are the triangles similar? Which theorem proves that they’re similar and complete the similarity statement.
???\triangle ABC\sim \triangle???____
We know from the figure that ???\angle A\cong\angle Z=76^\circ???. So we have a pair of congruent angles, and we need to see if we also have proportional side lengths.
???\frac{\overline{ZY}}{\overline{AC}}=\frac{18}{3}=6???
???\frac{\overline{ZX}}{\overline{AB}}=\frac{54}{9}=6???
We have the same ratio between corresponding side lengths.
Putting all this together, we can see say that the triangles are similar by Side Angle Side (SAS). When we match up the corresponding parts, the similarity statement is ???\triangle ABC\sim \triangle ZXY???.
Example
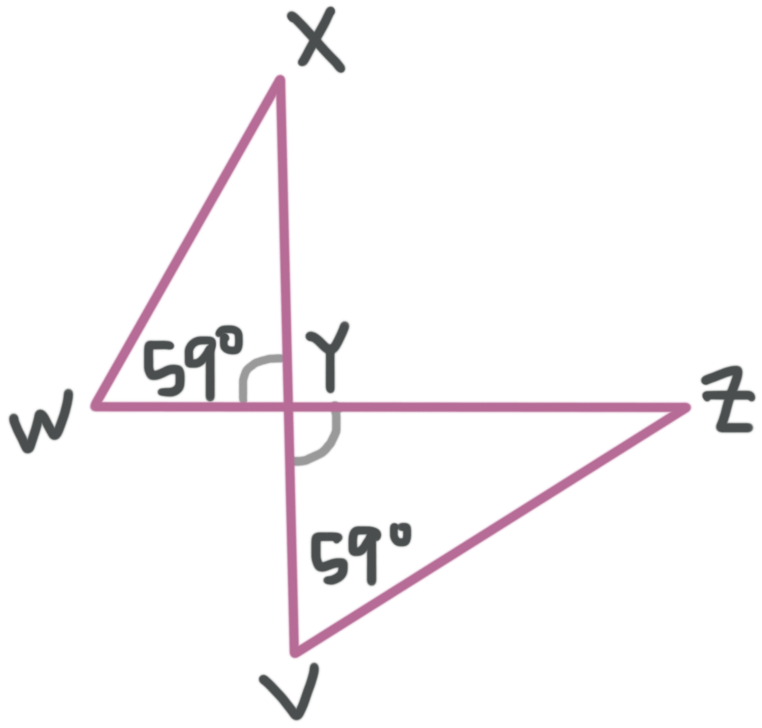
Are the triangles similar? Which theorem proves that they’re similar and complete the similarity statement.
???\triangle WXY\sim \triangle???____
We know from the figure that ???\angle W\cong\angle V=59^\circ???. We also have a pair of vertical angles at ???Y???, and remember that vertical angles are congruent to one another.
Putting all this together, we can see say that the triangles are similar by Angle Angle (AA). When we match up the corresponding parts, the similarity statement is ???\triangle WXY\sim \triangle VZY???.