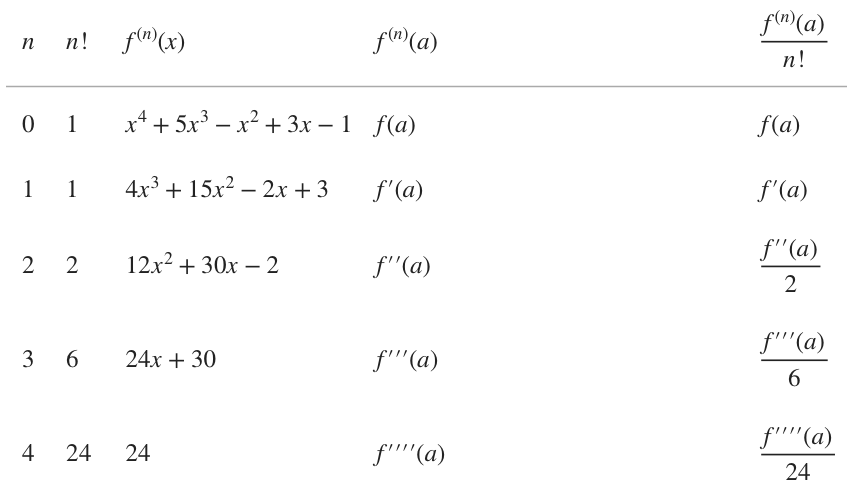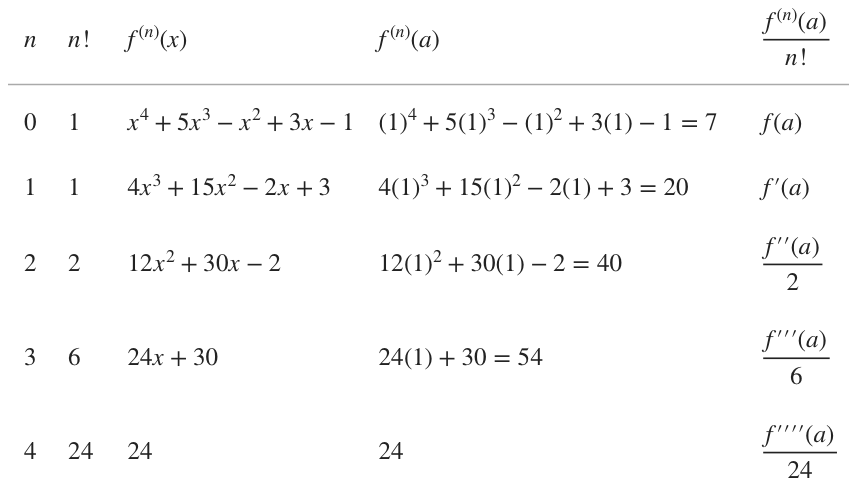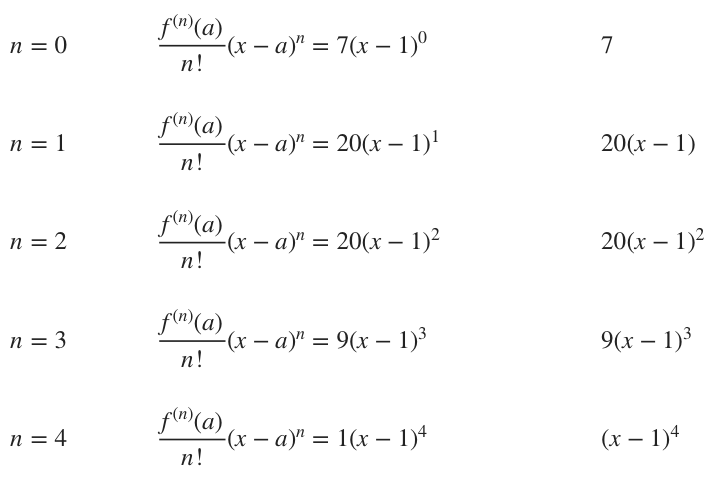How to build Taylor polynomials
Creating a Taylor series representation for a function
We already know how to use the power series
???\frac{1}{1-x}=\sum^{\infty}_{n=0}x^n???
to find a polynomial representation of a function.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
But sometimes we’ll want to represent a function as a series, and we won’t be able to easily relate the function to ???1/(1-x)???.
Taylor series let us find a series representation for any function, whether or not we can relate it to the power series ???1/(1-x)???.
In order to create a Taylor series representation for a function, we’ll need
???a??? - the value about which the function is defined
???n??? - the degree to which we want to evaluate the function
Both of these are usually given in the problem. With a value for ???a??? and ???n???, we can build the chart below.
When we’re done with the chart, the value in the far right column becomes the coefficient on each term in the Taylor polynomial, in the form
???\frac{f^{(n)}(a)}{n!}(x-a)^n???
The sum of all these terms is the Taylor series for the function.
How to build a third-degree Taylor polynomial (n=3) centered about ‘a’
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Using a chart to build a Taylor polynomial, one step at a time
Example
Find the fourth-degree taylor polynomial about ???a=1???.
???f(x)=x^4+5x^3-x^2+3x-1???
Since we’re looking for the fourth-degree polynomial, we can say that ???n=4???. As always, we’ll start ???n??? at ???0???, so the values of ???n??? we’ll include in our chart are ???n=0,1,2,3,4???. We can also include all of the corresponding values of ???n!???.
To find the values for the third column, we’ll put the original function in the first row, followed by its derivatives in the following rows.
Excerpt
To find the values for the fourth column, ???f^{(n)}(a)???, we’ll evaluate the values in the third column at ???a=1???.
To get the values for the last column, we’ll divide the result of the fourth column by ???n!??? from the second column.
With the whole chart filled in, we can build each term of the Taylor polynomial.
Putting all of the terms together, we get the fourth-degree taylor polynomial.
???7+20(x-1)+20(x-1)^2+9(x-1)^3+(x-1)^4???