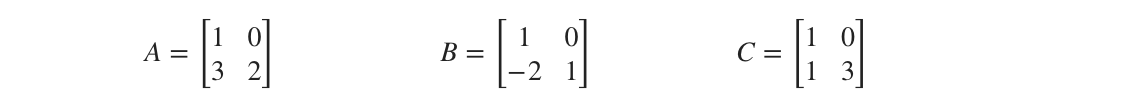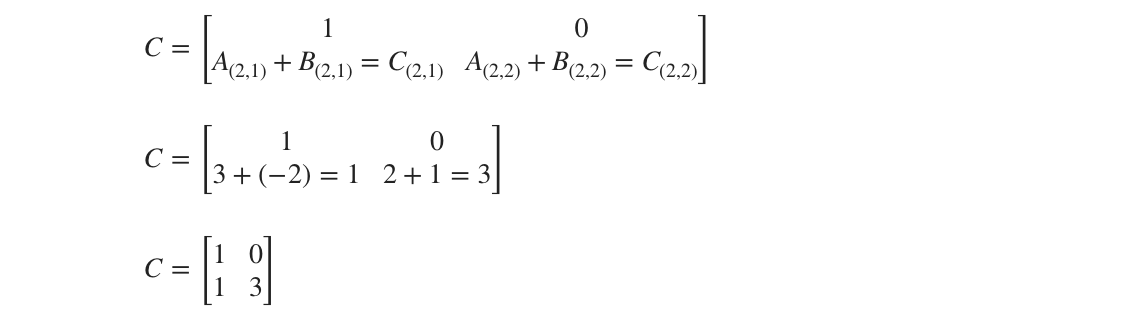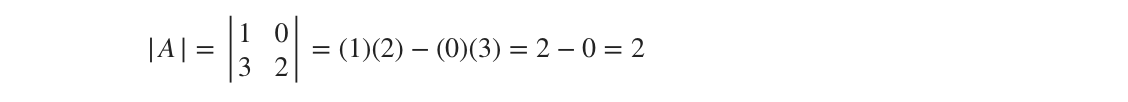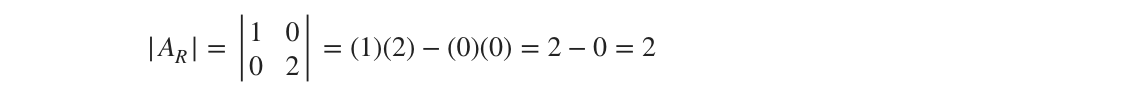Different ways of modifying determinants
Let’s talk about different operations we can do with the determinant
Now that we understand what the determinant is and how to calculate it, we want to look at other properties of determinants so that we can do more with them.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Multiplying a row or a column by a scalar
Given a square matrix ???A???, if you multiply one row (or one column) of ???A??? by a scalar ???k???, then the determinant just gets multiplied by ???k???. In other words, for a ???2\times2??? matrix
the determinant is ???|A|=ad-bc???. But if you multiply any row of ???A??? by a scalar ???k???, for instance
then the determinant is ???\text{Det}(B)=|B|=k|A|???, or ???k(ad-bc)???. It doesn’t matter which row you multiply by ???k???, the determinant will still be ???k(ad-bc)???. This also works for any ???n\times n??? matrix.
If you multiply ???n??? rows by the constant ???k???, then the determinant of the new matrix will be ???k^n|A|???. So if we’d multiplied both rows of ???A??? by ???k???,
then the determinant would have been ???\text{Det}(B)=|B|=k^2|A|???, or ???k^2(ad-bc)???.
Sum of two rows
When you have three identical matrices (and this works for any set of ???n\times n??? matrices, by the way), except that one row in each matrix is different, and that different row in the third matrix is the sum of the different rows from the first and second matrices, then we know the sum of the determinants of the first and second matrices is equal to the determinant of the third matrix.
For instance, these matrices ???A???, ???B???, and ???C??? all have an identical first row, but they have different second rows.
Furthermore, the second row in ???C??? is the sum of the second rows in ???A??? and ???B???.
When we have this specific case, ???|A|+|B|=|C|???.
???|A|+|B|=|C|???
???\begin{vmatrix}1 & 0\\ 3 & 2\end{vmatrix}+\begin{vmatrix}1 & 0\\ -2 & 1\end{vmatrix}=\begin{vmatrix}1 & 0\\ 1 & 3\end{vmatrix}???
???[(1)(2)-(0)(3)]+[(1)(1)-(0)(-2)]=[(1)(3)-(0)(1)]???
???(2-0)+(1-0)=(3-0)???
???2+1=3???
???3=3???
And like we said, this works the same way for any “different” row in the matrices, and for any set of these kinds of ???3\times3??? or ???n\times n??? matrices.
Swapped and duplicate rows
If you switch any row in a matrix ???A??? with any other row in the matrix ???A???, the determinant of the new “swapped-row matrix” ???B??? is equal to the negative determinant of ???A???. In other words,
???|B|=-|A|???
Let’s look at a simple example. If we start with the matrix ???A???,
then ???B??? is the matrix we get when we switch the rows.
Then based on this “swapped-row” rule, we should find ???|B|=-|A|???. Let’s see if we do.
???|B|=-|A|???
???\begin{vmatrix}3 & 2\\ 1 & 0\end{vmatrix}=-\begin{vmatrix}1 & 0\\ 3 & 2\end{vmatrix}???
???(3)(0)-(2)(1)=-[(1)(2)-(0)(3)]???
???0-2=-(2-0)???
???-2=-(2)???
???-2=-2???
This “swapped-row” rule obviously worked for our ???2\times2??? matrix, but it also works for any other ???3\times3??? or ???n\times n??? matrix.
But this rule creates one problem for us. Let’s say our matrix has two identical rows, and those are the two that we choose to swap. After we swap them, we end up with the same matrix we started with (???A=B???), since switching two identical rows isn’t going to do anything to change the matrix.
Which means that ???|A|=|B|???. But we’ve said that if we switch two rows, then ???|B|=-|A|???. From these two determinant equations, we’re saying that it must also be true that ???|A|=-|A|???. How is that possible? Well, the only way ???|A|=-|A|??? can be true is if the determinant is ???0???, because ???0??? is the only value that can satisfy an equation ???x=-x???.
So what does that tell us? It means that, if any ???n\times n??? matrix ???A??? has any two rows that are identical, then we know immediately, without doing any calculations, that its determinant is ???|A|=0???, or ???|A|=0???. The same is true if any ???n\times n??? matrix ???A??? has any two columns that are identical.
And as we know from before, if a matrix determinant is ???0???, then the matrix isn’t invertible, so we can say that any ???n\times n??? matrix with any two identical rows is not invertible, so its inverse isn’t defined.
Row operations don’t change the determinant
When we learned Gaussian elimination for solving systems, we learned how to use row operations to rewrite the matrix. It’s important to know that those row operations don’t change the value of the determinant, unless, of course, we’re multiplying by a scalar, which we talked about at the beginning of this lesson.
Modifying determinants by multiplying by a scalar, summing rows, and swapping rows
Take the course
Want to learn more about Linear Algebra? I have a step-by-step course for that. :)
Determining the effect of the row operation
Example
Verify that the row operation ???R_2-3R_1\to R_2??? doesn’t change the value of ???|A|???.
If we were trying to put this in reduced row-echelon form, we’d start with ???R_2-3R_1\to R_2???. The matrix ???A??? after the row operations would be
When you have three identical matrices, except that one row in each matrix is different, and that different row in the third matrix is the sum of the different rows from the first two matrices, then we know the sum of the determinants of the first two matrices is equal to the determinant of the third.
Row operations like these don’t change the value of ???|A|???. The determinant of ???A??? before the row operation is
And the determinant of ???A??? after the row operation is
We get the same value for the determinant in both cases.