How to graph exponential functions, step-by-step
Steps for sketching exponential functions
We also want to be able to graph exponential functions.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The kinds of functions we’re talking about are ones in which the variable is in the exponent, like these:
???y=3^{x}???
???y=-3^{x-1}-2???
???y=2\cdot\left(\frac{1}{3}\right)^{-x+2}-4???
???y=6\cdot2^{-x}+1???
In general, I like to follow a very consistent plan for graphing these kinds of equations.
Plug in ???x=100??? and ???x=-100??? to see what the function is doing as ???x??? starts getting close to ???-\infty??? or ???+\infty???.
One of these will result in an infinite value, the other will give a real-number value. The real-number value is the horizontal asymptote of the exponential function.
Plug in a few easy-to-calculate points, like ???x=-1,\ 0,\ 1??? in order to get a couple of points that we can plot.
Connect the points with an exponential curve, following the horizontal asymptote.
How to graph exponential functions
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Graphing exponential functions by plotting points, and using transformations
Example
Graph the exponential function.
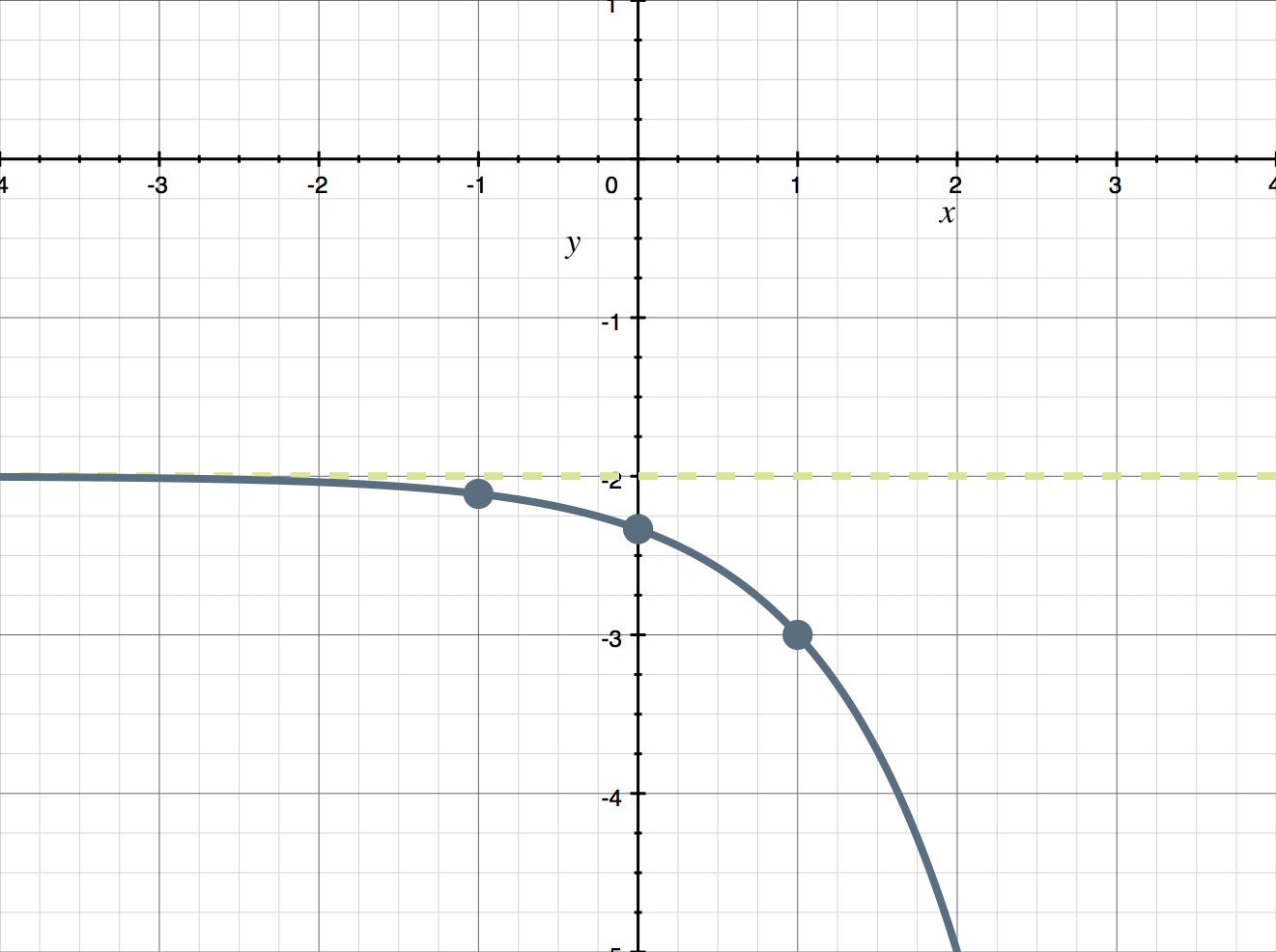
???y=-3^{x-1}-2???
We’ll start by plugging in ???x=100??? and ???x=-100???.
For ???x=100???:
???y=-3^{100-1}-2???
???y=-3^{99}-2???
???y=-(\text{very large positive number})-2???
???y=\text{very large negative number}-2???
???y=\text{very large negative number}???
???y=-\infty???
For ???x=-100???:
???y=-3^{-100-1}-2???
???y=-3^{-101}-2???
???y=-\frac{1}{3^{101}}-2???
???y=-\frac{1}{\text{very large positive number}}-2???
???y=-(0)-2???
???y=0-2???
???y=-2???
This basically allowed us to evaluate end behavior, and we’ve learned that the function has a horizontal asymptote at ???y=-2???, and heads down toward ???-\infty??? as ???x??? gets very large.
We’ll plug in a few simple-to-evaluate values for ???x???.
For ???x=0???:
???y=-3^{0-1}-2???
???y=-3^{-1}-2???
???y=-\frac{1}{3^1}-2???
???y=-\frac{1}{3}-\frac{6}{3}???
???y=-\frac{7}{3}???
For ???x=-1???:
???y=-3^{-1-1}-2???
???y=-3^{-2}-2???
???y=-\frac{1}{3^{2}}-2???
???y=-\frac{1}{9}-\frac{18}{9}???
???y=-\frac{19}{9}???
For ???x=1???:
???y=-3^{1-1}-2???
???y=-3^{0}-2???
???y=-1-2???
???y=-3???
Now we have three points on the graph of the exponential function, ???(0,-7/3)???, ???(-1,-19/9)???, and ???(1,-3)???. If we plot these three points, and the horizontal asymptote ???y=-2???, we get
Based on the asymptote, and the points we’ve found, we can already see what the graph is going to do. We’ll simply connect the points to sketch the graph.
Sometimes we’re given the graph of one exponential function, and asked to sketch a graph of a similar function which is just a few transformations away from the given function.
One of these will result in an infinite value, the other will give a real-number value. The real-number value is the horizontal asymptote of the exponential function.
Example
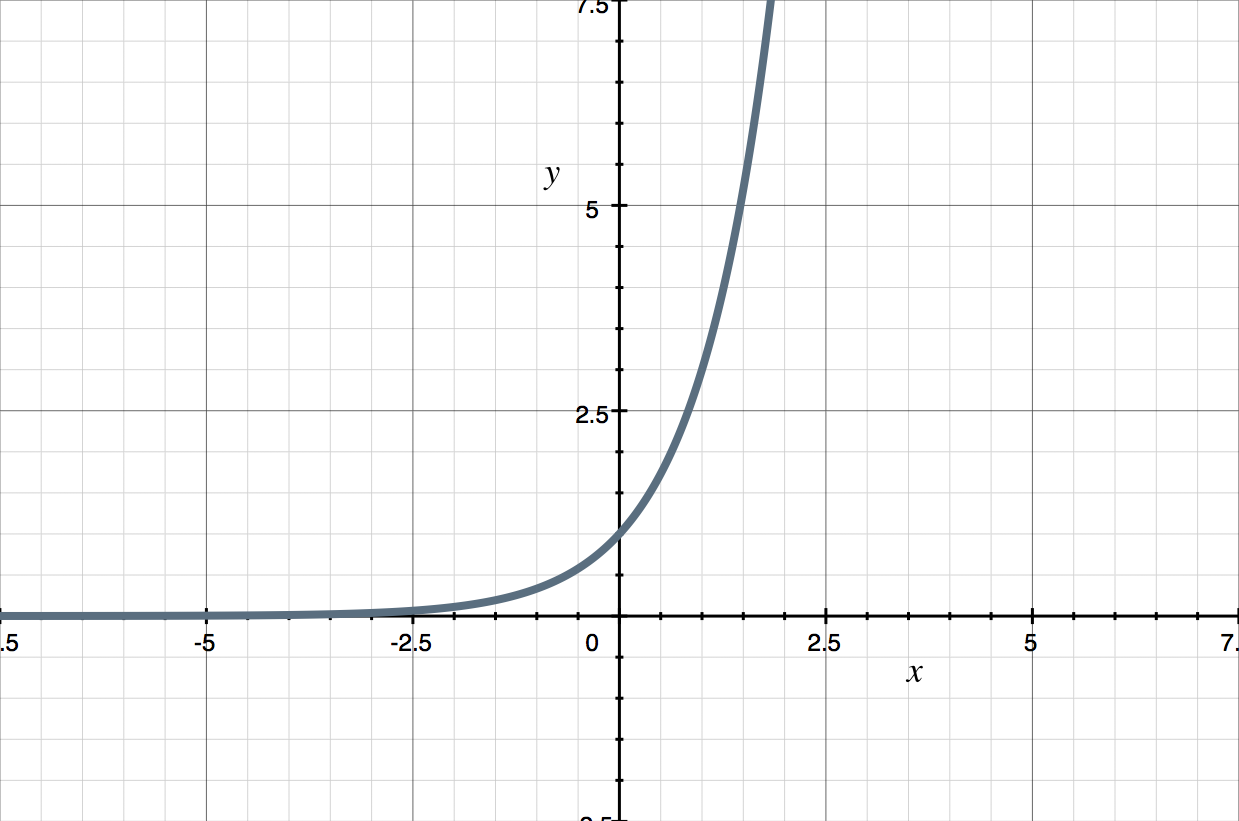
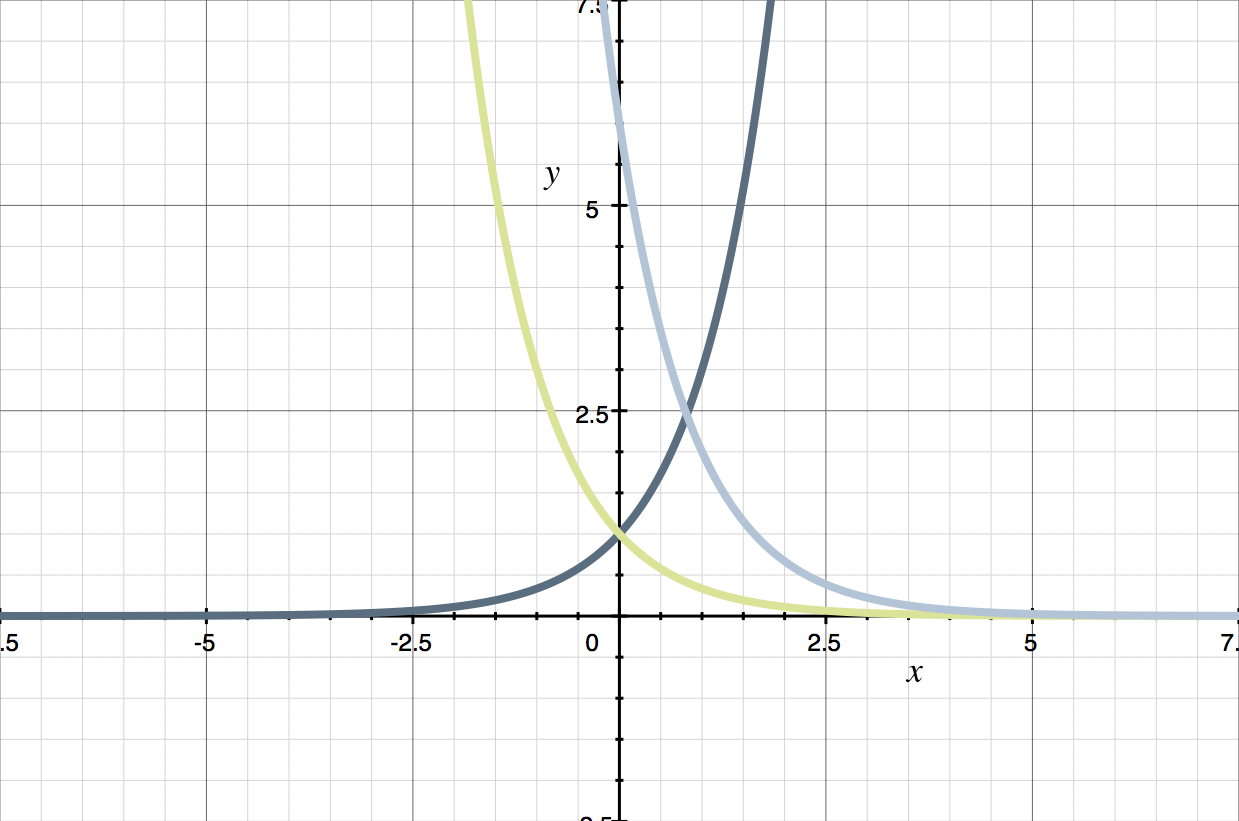
The graph of ???y=3^{x}??? is shown. Use this graph to sketch a graph for ???y=6\cdot3^{-x}+1???.
Both functions are based on the standard ???y=3^{x}??? function. The function ???y=6\cdot3^{-x}+1??? has simply undergone several transformations. We want to break up the transformations so that we show each transformation in its own step.
[1] ???y=3^{x}???
[2] ???y=3^{-x}???
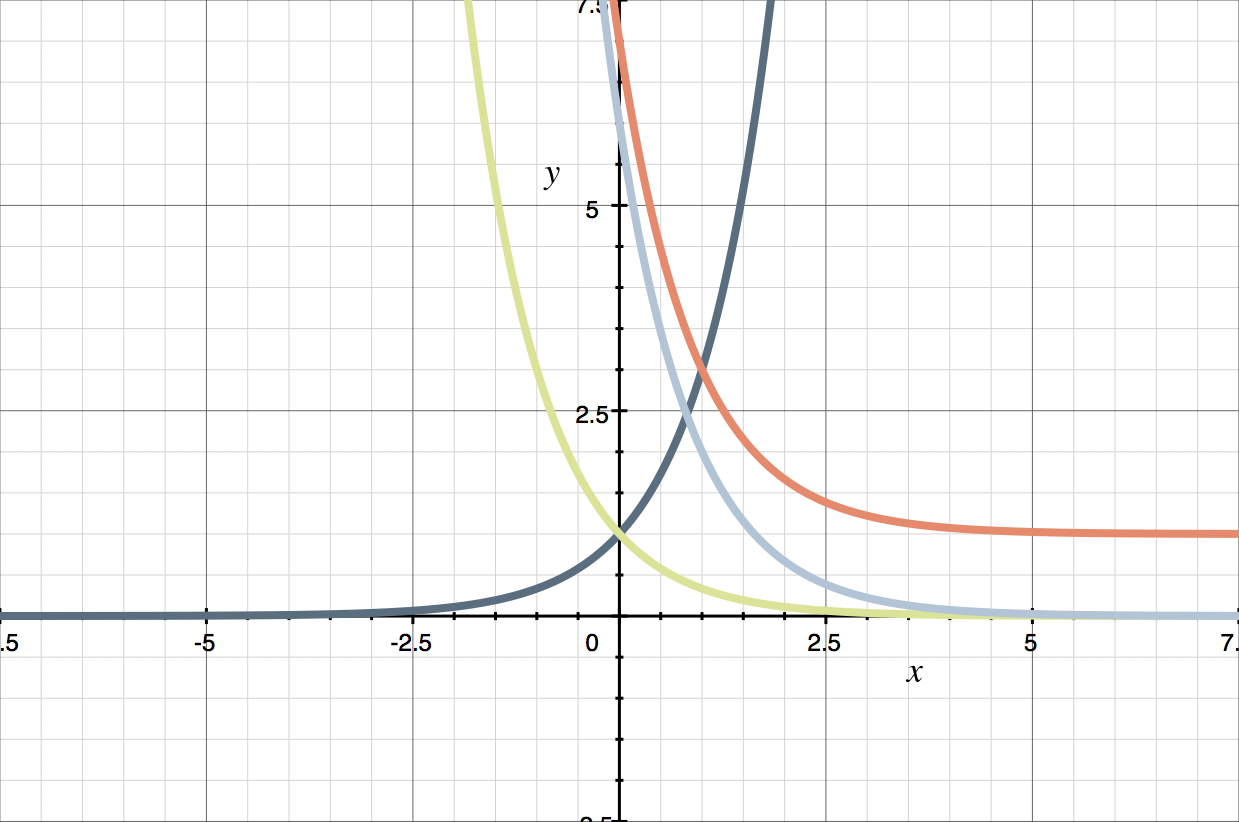
[3] ???y=6\cdot3^{-x}???
[4] ???y=6\cdot3^{-x}+1???
We were given the graph of [1] ???y=3^{x}???.
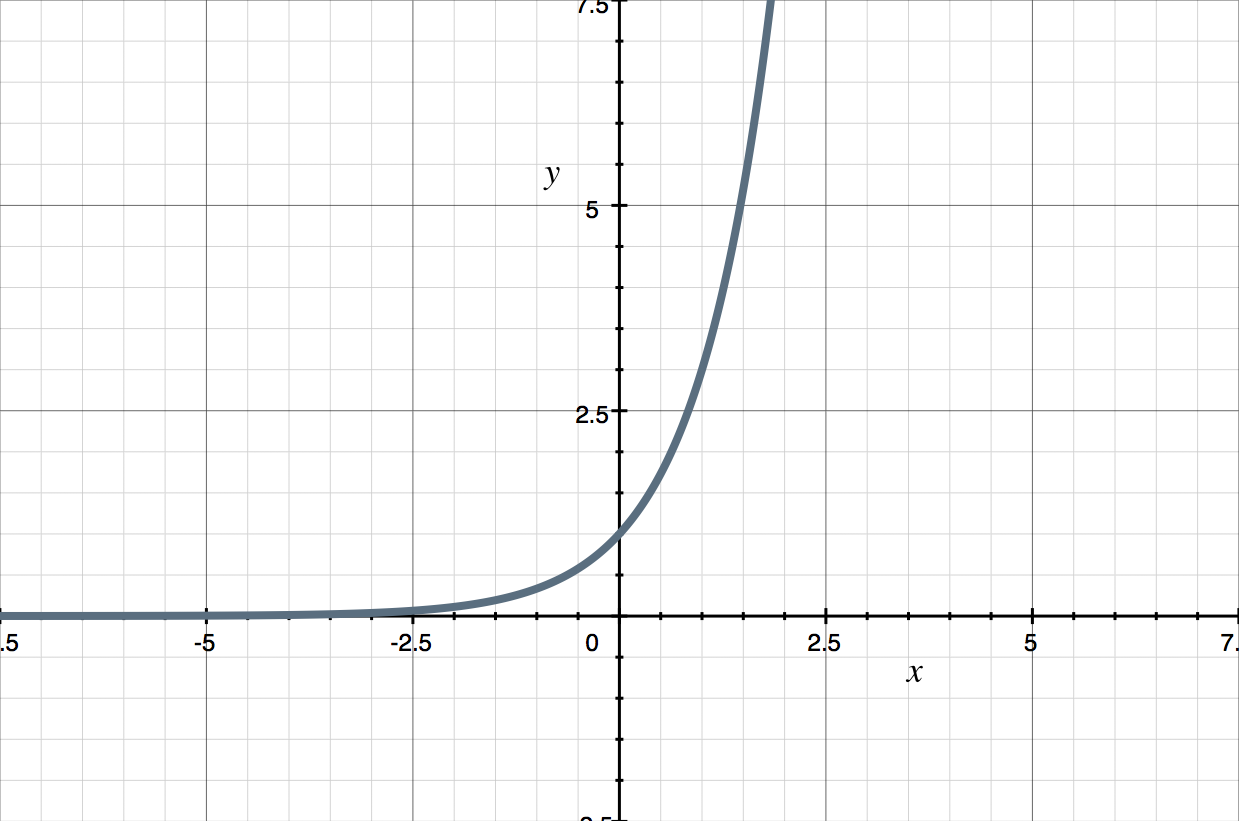
If we change the ???x??? into ???-x???, that means we’re reflecting the graph over the ???y???-axis. If you’re not sure about this, try plugging a few points into ???y=3^{-x}???. If we plot [2] ???y=3^{-x}??? on the same set of axes, we get
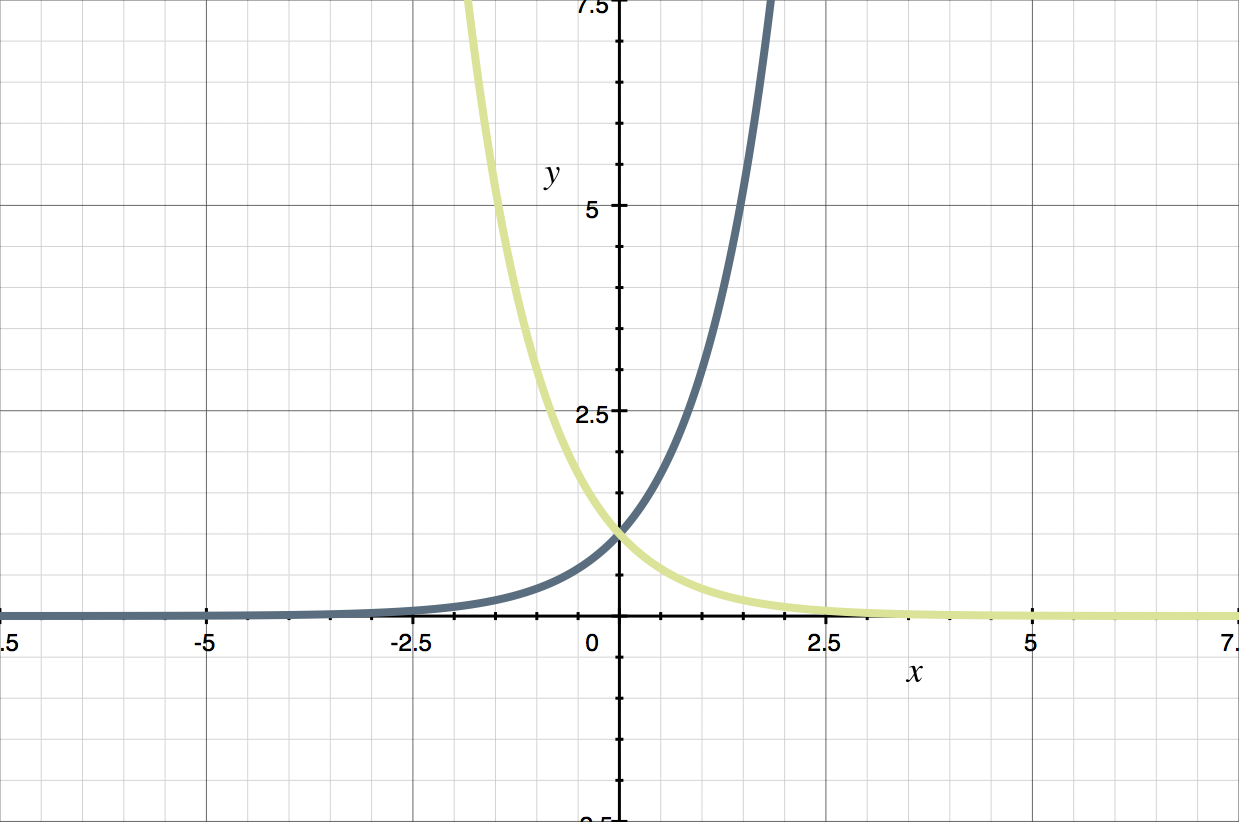
Multiplying by ???6??? means that each value of ???y=3^{-x}??? gets multiplied by ???6???. So, since ???y=3^{-x}??? crosses the ???y???-axis at ???1???, [3] ???y=6\cdot3^{-x}??? crosses the ???y???-axis at ???1\cdot6=6???.
Adding ???1??? means that each value of ???y=6\cdot3^{-x}??? gets shifted vertically upward by ???1???. So since ???y=6\cdot3^{-x}??? crosses the ???y???-axis at ???6???, [4] ???y=6\cdot3^{-x}+1??? crosses the ???y???-axis at ???6+1=7???.
To summarize, we started with ???y=3^{x}??? and its graph, and were able to undergo one transformation at a time,
[1] ???y=3^{x}???
[2] ???y=3^{-x}???
[3] ???y=6\cdot3^{-x}???
[4] ???y=6\cdot3^{-x}+1???
to eventually get to the graph of ???y=6\cdot3^{-x}+1???.