Finding the work required to empty a tank

How to find the work required to empty a tank

Finding the work required to empty a tank of the substance it contains is a common calculus application.

We always solve these problems the same way.

1. We divide the tank into an infinite number of slices $n$.

2. We calculate the work required to remove that single slice of substance from the tank.

3. We develop an equation to solve for the work needed to empty the entire tank, based on the work that was required to remove the single slice.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

While this process seems fairly simple, it’ll take a little effort to calculate the work required to remove a single slice of substance.

We know that work is equal to force multiplied by distance ($W=Fd$), so we’ll find force and distance, and then use them to find work. To get force, we use the equation $F=mg$, where $m$ is mass and $g$ is the gravitational constant, $g=9.8$ m/s$^2$.

To solve for mass, we’ll remember that mass is equal to density multiplied by volume $m=\delta V$.

Density of the substance in the tank is usually provided in the problem, or the substance in the tank is water, which has a known density of $1,000$ kg/m$^3$. Volume of the single slice will depend on the shape of the tank.

As you can see, we’ll start by calculating the most basic pieces of information, and then work our way up to finding work. In other words, follow these steps:

1. Find density and volume, then use them to calculate mass.

2. Multiply mass by the gravitational constant to find force.

3. Multiply force by distance to get work.

Remember that it’s extremely useful to draw a diagram of the tank and the substance inside, labeling everything we know, before we start making calculations.

Video example of finding the work required to empty a tank of its fluid

---

Take the course

Want to learn more about Calculus 2? I have a step-by-step course for that. :)

---

Finding the work required to empty an inverted circular cone that’s filled with water

Example

A tank in the shape of an inverted circular cone has a height of $10$ m and base radius of $5$ m. It’s filled with water to a height of $7$ m. Find the work required to empty the tank by pumping the water out through the top. Remember, the density of water is $1,000$ kg/m$^3$.

We’ll always start by drawing a diagram first.

If the height of the water is $7$ m, then the top $3$ m of the tank is empty. We want to divide the water into $n$ slices, figure out the work required to lift one slice, and then add the work for all of the slices together.

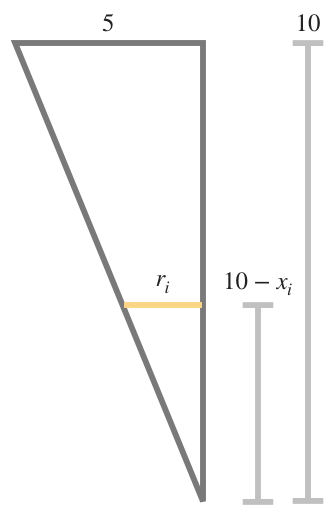
One slice has a height of $\Delta{x}$. We can call the radius of this slice $r_i$. We can also say that the distance from the slice to the top of the tank is $x_i$.

Following the three steps given above, we need to find density and volume, then use them to calculate mass. We know that the density of water is $\delta =1,000$ kg/m$^3$. Volume of the circular slice is given by the formula for the volume of a cylinder.

$V_i=(\text{circular area})(\text{height})$

$V_i=\left(\pi{r^2_i}\right)\left(\Delta{x}\right)$

$V_i=\pi{r^2_i}\Delta{x}$

In order to get a real value for volume, we need to solve for the radius $r_i$. To solve for the radius we can use the property of similar triangles.

The diagram below shows how a triangular section of the entire tank relates to the the triangular section underneath the slice.

If we know that the height of the tank is $10$ m, and if we know (from the last diagram) that the distance between the slice and the top of the tank is $x_i$, then that means the distance between the slice and the bottom of the tank is $10-x_i$.

Let’s set up the equation for $r_i$ using the property of similar triangles, which tells us that the following ratios are equal:

$\frac{r_i}{10-x_i}=\frac{5}{10}$

$r_i=\frac12(10-x_i)$

Next we’ll solve for volume using $V_i=\pi{r^2_i}\Delta{x}$ and the value we just found for $r_i$.

$V_i=\pi{r^2_i}\Delta{x}$

$V_i=\pi{\left[\frac12(10-x_i)\right]^2}\Delta{x}$

$V_i=\frac{\pi}{4}(10-x_i)^2\Delta{x}$

Now that we finally have the volume, we can multiply it by the density to get an equation for mass.

$m=\delta V$

$m_i=(1,000)\left[\frac{\pi}{4}(10-x_i)^2\Delta{x}\right]$

$m_i=250\pi(10-x_i)^2\Delta{x}$

With a value for mass, we can calculate force using $F_i=m_ig$ and $g=9.8$ m/s$^2$.

$F_i=m_ig$

$F_i=\left[250\pi(10-x_i)^2\Delta{x}\right](9.8)$

$F_i=2,450\pi(10-x_i)^2\Delta{x}$

With a value for force, we can calculate work using $W_i=F_id$. Remember that the distance from the slice to the top of the tank is $x_i$.

$W_i=F_id$

$W_i=\left[2,450\pi(10-x_i)^2\Delta{x}\right](x_i)$

$W_i=2,450\pi{x_i}(10-x_i)^2\Delta{x}$

we’ll start by calculating the most basic pieces of information, and then work our way up to finding work.

At this point we have an equation for the work required to lift a single slice of the water to the top of the tank to remove it. Our next step is to modify the work equation we just found so that it models the work required to remove all the water from the tank (all $n$ slices), not just a single slice.

In order to get the most accurate result, we want to use as many slices as possible, which means we’ll take $n\rightarrow\infty$. In other words, we’ll take the limit as $n\rightarrow\infty$ of the work equation that sums up the work required for all the slices, and we get

$W=\lim_{n\to\infty}\sum_{i=1}^n2,450\pi{x_i}(10-x_i)^2\Delta{x}$

Of course, this is the same thing as taking the integral over the given interval. Since we’re now looking at all values of $x$, we can let $x_i=x$. Since we’re changing to integral notation, we also let $\Delta x=dx$. The interval of integration is $[3,10]$ because the top-most slice of water has to be lifted $3$ m to be removed from the tank, and the bottom-most slice of water has to be lifted $10$ m to be removed from the tank.

$W=\int^{10}_32,450\pi{x}(10-x)^2\ dx$

$W=2,450\pi\int^{10}_3x(10-x)^2\ dx$

$W=2,450\pi\int^{10}_3100x-20x^2+x^3\ dx$

$W=2,450\pi\left[50x^2-\frac{20x^3}{3}+\frac{x^4}{4}\right]\bigg|^{10}_3$

$W=2,450\pi\left[50(10)^2-\frac{20(10)^3}{3}+\frac{(10)^4}{4}\right]-2,450\pi\left[50(3)^2-\frac{20(3)^3}{3}+\frac{(3)^4}{4}\right]$

$W=4,179,802.6$

$W=4.18\times10^6$

The work required to empty the tank is $4.18\times10^6$ J.

---

Get access to the complete Calculus 2 course

---